সকল কোণের মান .... শূন্য

০২ রা নভেম্বর, ২০১৩ রাত ৩:৪৭

গণিতে অন্যতম মজার ব্যাপার হলো প্যারাডক্স আর Fallacy. যারা এই ব্যাপারগুলো জানেন তারা বোঝবেন সামান্য একটু নিয়মের বাইরে গিয়ে কত অসম্ভব প্রমাণ গণিতের সাহায্যে করা যায়। তার আগে Fallacy শব্দটার সাথে যারা পরিচিত নন তাদের বলে নেই, Fallacy মানে গাণিতিকভাবে সেই সব ভুল সিদ্ধান্ত যাদের ক্ষেত্রে যুক্তি (প্রায়) সঠিক।



এখন আমরা সেইরকম একটি Fallacy দেখবো। খুব সহজ আর মজার তো অবশ্যই।







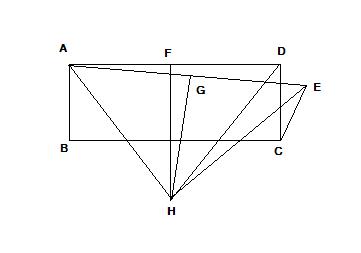
চিত্রটি খেয়াল করি

এখানে ABCD একটি আয়তক্ষেত্র। এবার যেকোন কোণ DCE আঁকি যেন CD = CE হয়। ধরি, AD ও AE এর সমদ্বিখণ্ডকদ্বয় H বিন্দুতে ছেদ করে।

যেহেতু H, AD এর লম্ব সমদ্বিখণ্ডকের উপর অবস্থিত,

তাই, AH = HD.

আবার H কিন্তু AE এর সমদ্বিখণ্ডকের উপরও অবস্থিত, তাই

AH = HE

So, HD = HE

এখন ∆ DCH ও ∆ ECH-এ

HD = HE

CD = CE

এবং CH সাধারণ বাহু।

তাহলে, ∆ DCH ও ∆ ECH সর্বসম।

অর্থাৎ, কোণ DCH = কোণ ECH

So, কোণ DCE = কোণ ECH - কোণ DCH = 0



যেহেতু যেকোন কোণ DCE এর জন্যই এটি (আপাতত) সত্য সেজন্য বলা যেতে পারে, যেকোন কোণই শূন্য।



গাণিতিকভাবে ভুল একটি প্রমাণ। এখন ভুলটা ধরাই হচ্ছে আসল কথা। আরেকটা কথা ভুলটা আমি অবশ্যই বলছি না।

৩ টি +০/-০