সংখ্যা বিলাস- ২ঃ একটি ইউজলেস সংখ্যার গল্প।

১৫ ই জুলাই, ২০১৬ সন্ধ্যা ৬:৫৮

সেই ষোড়শ শতাব্দীর কথা।
ইতালিয়ান গণিতবিদেরা তখন ব্যস্ত কিউবিক পলিনমিনাল ফাংশন তথা ঘনমূলীয় বহুপদী ফাংশান নিয়ে।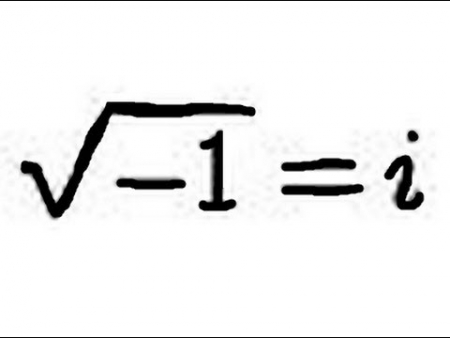

ঘনমূলীয় বহুপদী ফাংশানটির গ্রাফ আঁকালে দেখতে হয় নিচের ছবিটির মত।ফাংশানটির সমাধান পাওয়া যায় ১ টি অথবা ৩ টি যা নির্ভর করে ধ্রুবকের উপর।


যদি ধরি রেখাটি কোথাও X অক্ষকে ছেদ করে ,তবে ফাংশান=০ ধরে এর সমাধান করা যায়। নিচের এই ছবিটির মত।


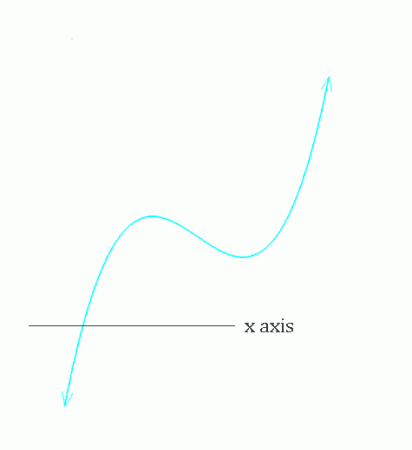
কিন্তুু ধ্রুবক পরিবর্তন করে যদি নিচের গ্রাফের মত লেখ আঁকেন তাহলে ?


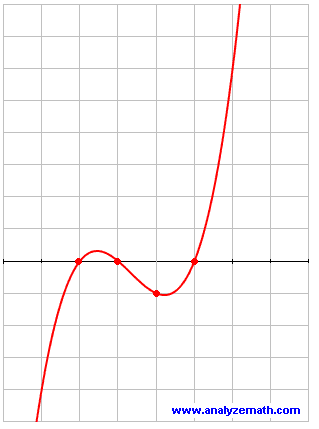
এক্ষেত্রে কিন্তু সমাধান ৩ টি। সমাধানগুলিও একটু জটিল হয়ে উঠে। এধরনের লেখের সমাধান করতে গিয়ে মাথায় হাত পরে তখনকার ইতালীয় গনিতবিদদের। এমন না যে তারা এর সমাধান করতে পারছিলেন না , ব্যাপারটি হল সমাধান কিভাবে হল তারা তা বুঝতে পারছিলেন না।


জেরলামো কারদানো নামের এক গনিতবিদ প্রথম এর সমাধান করেন। সমাধানের একটি পর্যায়ে তিনি {5+(√-15)}.{5-(√-15) } ব্যবহার করে সমাধানটি সম্পন্ন করেন। এই সমাধান নিয়ে তিনি লিখেছিলেন "Multiplying (5+√-15) by (5-√-15) we obtain 25-(-15) and therefore the product is 40 and thus far does arithmetical subtlety go of which this the extreme is as i have said,so subtle that it is useless"। (হাসতে হাসতে কাইন্দালছি ইমোজি)।

এতক্ষন কি নিয়ে গ্যাজাচ্ছি আন্দাজ করতে পেরেছেন মনে হয়, কাল্পনিক তথা ইমাজিনারি নাম্বার। ষোড়শ শতাব্দীতে এর ব্যবহার এতই সীমিত ছিল যে সেই ইতালিয় গনিতবিদ একে 'ইউজলেস নাম্বার' নাম্বার হিসেবে ঘোষণা করে বসেন। তিনি যদি জানতেন এই ইউজলেস নাম্বারের ব্যবহার ছাড়া ইলেক্ট্রিক্যাল ডিভাইসগুলির সার্কিট ডিজাইন সম্ভব হত না অথবা অ্যারোনোটিকাল ইঞ্জিনিয়ারিং এতদূর আসত না আর দেখতেন এছাড়াও বিভিন্ন ইঞ্জিনিয়ারিং ক্ষেত্রে এর বহুল ব্যবহার আছে তাহলে হয়ত এই 'ইউজলেস নাম্বার' টিকে ঠিকই সরি বলতেন। (হাসির ইমোজি)

৩ টি +১/-০