অয়লারের কোণ

০৫ ই মার্চ, ২০২৩ সকাল ৮:২৪

অয়লারের কোণ:

অয়লারের কোণগুলি তিনটি ভিন্ন অক্ষের চারপাশে তিনটি ঘূর্ণন ব্যবহার করে ত্রিমাত্রিক স্থানের একটি বস্তুর অভিযোজন বর্ণনা করার একটি উপায়। তিনটি ঘূর্ণনকে সাধারণত পিচ, ইয়াও এবং রোল বলা হয় এবং এগুলি একটি নির্দিষ্ট ক্রমে প্রয়োগ করা হয়। ঘূর্ণনের ক্রম ব্যবহৃত কনভেনশনের উপর নির্ভর করে পরিবর্তিত হতে পারে, তবে সবচেয়ে সাধারণ কনভেনশন হল "ZYX" কনভেনশন, যার অর্থ হল ঘূর্ণনগুলি ইয়াও, পিচ এবং রোলের ক্রমে প্রয়োগ করা হয়। অয়লারের কোণগুলির পদার্থবিদ্যা, প্রকৌশল এবং কম্পিউটার গ্রাফিক্সে অনেকগুলি প্রয়োগ রয়েছে, কিন্তু তারা কিছু নির্দিষ্ট সীমাবদ্ধতা এবং অস্পষ্টতার প্রবণ হতে পারে, যেমন জিম্বাল লক, যা ঘটবে যখন দুটি ঘূর্ণন অক্ষ সারিবদ্ধ হয়ে যায় এবং এক ডিগ্রি স্বাধীনতা হারিয়ে যায়।

অয়লারের কোণ সামারিঃ

অয়লারের কোণগুলি একটি নির্দিষ্ট স্থানাঙ্ক ব্যবস্থার সাথে 3D স্পেসে একটি কঠোর বডির অভিযোজন উপস্থাপন করতে ব্যবহৃত তিনটি কোণের একটি সেট। তিনটি কোণকে সাধারণত পিচ, ইয়াও এবং রোল হিসাবে চিহ্নিত করা হয় এবং তারা তিনটি স্বতন্ত্র অক্ষের চারপাশে ঘূর্ণন উপস্থাপন করে।

অয়লার কোণগুলি প্রকৌশল, পদার্থবিদ্যা এবং কম্পিউটার গ্রাফিক্সে ব্যাপকভাবে ব্যবহৃত হয়, তবে তাদের কিছু সীমাবদ্ধতা রয়েছে, যেমন এককতা এবং উপস্থাপনার অ-স্বতন্ত্রতা। বিকল্প উপস্থাপনা, যেমন কোয়াটার্নিয়ন, এই সমস্যাগুলি সমাধানের জন্য তৈরি করা হয়েছে।

তাদের সীমাবদ্ধতা সত্ত্বেও, অয়লার অ্যাঙ্গেলগুলি রোবোটিক্স, মহাকাশ প্রকৌশল এবং কম্পিউটার অ্যানিমেশন সহ অনেক অ্যাপ্লিকেশনের জন্য একটি দরকারী টুল হিসাবে রয়ে গেছে।



অয়লারের তিনটি কোণ:


অয়লারের তিনটি কোণ হল তিনটি কোণের একটি সেট যা একটি স্থির স্থানাঙ্ক ব্যবস্থার সাপেক্ষে 3D স্পেসে একটি রিজিড বডির অভিযোজন বর্ণনা করে। তিনটি কোণকে সাধারণত φ (phi), θ (থিটা), এবং ψ (psi) হিসাবে চিহ্নিত করা হয় এবং তারা তিনটি স্বতন্ত্র অক্ষের চারপাশে ঘূর্ণন উপস্থাপন করে।

বিশেষভাবে, φ শরীরের x-অক্ষের ঘূর্ণনকে প্রতিনিধিত্ব করে, θ শরীরের y-অক্ষের ঘূর্ণনকে প্রতিনিধিত্ব করে এবং ψ শরীরের z-অক্ষের ঘূর্ণনকে প্রতিনিধিত্ব করে। এই ঘূর্ণনগুলি যে ক্রমানুসারে প্রয়োগ করা হয় তা পরিবর্তিত হতে পারে, ফলে বিভিন্ন নিয়ম যেমন ZYX কনভেনশন, যা ঘূর্ণনগুলিকে ψ-θ-φ ক্রমে প্রয়োগ করে।

অয়লারের তিনটি কোণ প্রকৌশল, পদার্থবিদ্যা এবং কম্পিউটার গ্রাফিক্সে ব্যাপকভাবে ব্যবহৃত হয়, তবে তাদের কিছু সীমাবদ্ধতা রয়েছে, যেমন এককতা এবং উপস্থাপনার অ-স্বতন্ত্রতা। বিকল্প উপস্থাপনা, যেমন কোয়াটার্নিয়ন, এই সমস্যাগুলি সমাধানের জন্য তৈরি করা হয়েছে।

অয়লারের ম্যাট্রিক্স:

অয়লারের ম্যাট্রিক্স হল একটি 3x3 ঘূর্ণন ম্যাট্রিক্স যা একটি নির্দিষ্ট স্থানাঙ্ক সিস্টেমের সাথে 3D স্পেসে একটি রিজিড বডির অভিযোজন বর্ণনা করে। ম্যাট্রিক্সটি তিনটি পৃথক ঘূর্ণন ম্যাট্রিক্সকে গুণ করে তৈরি করা হয় যা শরীরের x, y এবং z অক্ষের চারপাশে ঘূর্ণনকে প্রতিনিধিত্ব করে।

অয়লারের ম্যাট্রিক্স অয়লারের তিনটি কোণ থেকে উদ্ভূত হতে পারে, যা একই ঘূর্ণনকে উপস্থাপন করে কিন্তু ভিন্ন আকারে। কম্পিউটার গ্রাফিক্স এবং রোবোটিক্সের মতো ঘূর্ণনগুলির দক্ষ গণনা প্রয়োজন এমন অ্যাপ্লিকেশনগুলিতে ম্যাট্রিক্সটি কার্যকর। যাইহোক, এর কিছু সীমাবদ্ধতা রয়েছে, যেমন এককতা এবং প্রতিনিধিত্বের অ-স্বতন্ত্রতা, যা বিকল্প উপস্থাপনা যেমন quaternions ব্যবহার করে সমাধান করা যেতে পারে।



সম্পূর্ণ ঘূর্ণন:

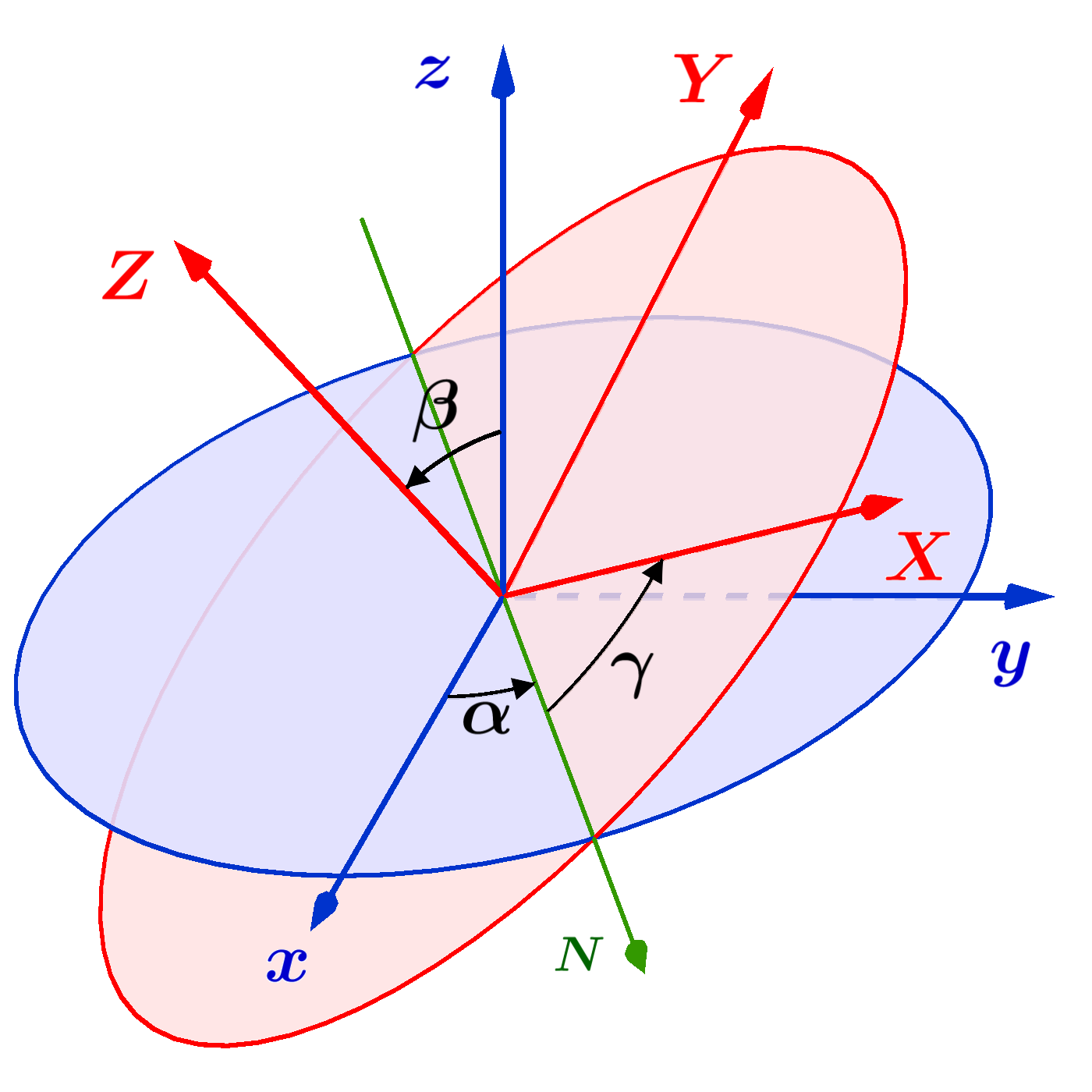
অয়লার কোণ ব্যবহার করে একটি সম্পূর্ণ ঘূর্ণন উপস্থাপন করতে, আমরা সাধারণত তিনটি কোণ ব্যবহার করি, যা α, β এবং γ হিসাবে চিহ্নিত করা হয়। প্রথম ঘূর্ণনটি একটি কোণ α দ্বারা z-অক্ষের চারপাশে, দ্বিতীয় ঘূর্ণনটি একটি কোণ β দ্বারা নতুন y-অক্ষের চারপাশে এবং তৃতীয় ঘূর্ণনটি একটি কোণ γ দ্বারা নতুন z-অক্ষের চারপাশে। রিজিড বডির ফলশ্রুতিতে একটি 3x3 ঘূর্ণন ম্যাট্রিক্স দ্বারা প্রতিনিধিত্ব করা যেতে পারে, এটি একটি ম্যাট্রিক্স যা একটি ভেক্টরের স্থানাঙ্কগুলিকে মূল স্থানাঙ্ক সিস্টেম থেকে ঘূর্ণিত স্থানাঙ্ক সিস্টেমে রূপান্তরিত করে।


বডি ফ্রেমঃ

অয়লার অ্যাঙ্গেলের প্রেক্ষাপটে, বডি ফ্রেমটি স্থানাঙ্ক সিস্টেমকে বোঝায় যা রিজিড বডি ঘোরানো অবস্থায় স্থির থাকে। বডি ফ্রেমের ওরিয়েন্টেশন তিনটি অয়লার অ্যাঙ্গেল দ্বারা বর্ণনা করা হয়, যা নির্দিষ্ট রেফারেন্স ফ্রেমের সাথে বডি ফ্রেমকে সারিবদ্ধকরণে আনতে প্রয়োজনীয় ঘূর্ণনগুলি নির্দিষ্ট করে (এটি গ্লোবাল ফ্রেম বা বিশ্ব ফ্রেম নামেও পরিচিত)।

বডি ফ্রেম হল একটি স্থানীয় সমন্বয় ব্যবস্থা, যার মানে গ্লোবাল ফ্রেমের সাপেক্ষে এর ওরিয়েন্টেশন এবং অবস্থান পরিবর্তিত হতে পারে। উদাহরণস্বরূপ, যদি আমরা পৃথিবীর চারপাশে কক্ষপথে একটি মহাকাশযানের কল্পনা করি, তাহলে মহাকাশযানের বডি ফ্রেমটি মহাকাশযানের সাথেই স্থির হয়ে যাবে এবং মহাকাশযানটি নড়াচড়া করার সাথে সাথে ঘুরবে। এদিকে, গ্লোবাল ফ্রেম পৃথিবীতে স্থির হবে এবং মহাকাশযানের তুলনায় স্থির থাকবে।

অয়লার অ্যাঙ্গেল, যেমন বিমান এবং মহাকাশযান নিয়ন্ত্রণ, রোবোটিক্স এবং কম্পিউটার গ্রাফিক্স জড়িত অনেক অ্যাপ্লিকেশনে বডি ফ্রেম একটি গুরুত্বপূর্ণ ধারণা। এই অ্যাপ্লিকেশনগুলিতে, বডি ফ্রেমটি নিয়ন্ত্রিত বা রেন্ডার করা বস্তুর অবস্থান এবং অভিযোজন নির্ধারণ করতে ব্যবহৃত হয় এবং অয়লার কোণগুলি পছন্দসই অভিযোজন অর্জনের জন্য প্রয়োজনীয় ঘূর্ণনগুলি নির্দিষ্ট করতে ব্যবহৃত হয়।



রিজিড বডি:
পদার্থবিজ্ঞানে, একটি রিজিড বডি (একটি রিজিড বস্তু নামেও পরিচিত) হল একটি কঠিন বডি যেখানে বিকৃতি শূন্য বা এত ছোট এটিকে উপেক্ষা করা যেতে পারে। একটি রিজিড বডি তে যে কোনো দুটি প্রদত্ত বিন্দুর মধ্যে দূরত্ব বাহ্যিক শক্তি বা মুহূর্ত নির্বিশেষে স্থির থাকে। একটি রিজিড বডিকে সাধারণত ভরের অবিচ্ছিন্ন বন্টন হিসাবে বিবেচনা করা হয়।
বিশেষ আপেক্ষিকতার গবেষণায়, একটি পুরোপুরি রিজিড বডির অস্তিত্ব নেই; এবং বস্তুগুলিকে শুধুমাত্র রিজিড বলে ধরে নেওয়া যেতে পারে যদি তারা আলোর গতির কাছাকাছি না চলে। কোয়ান্টাম মেকানিক্সে, একটি রিজিড বডিকে সাধারণত বিন্দু ভরের একটি সংগ্রহ হিসাবে ভাবা হয়। উদাহরণ স্বরূপ, অণুগুলি (বিন্দু ভর নিয়ে গঠিত: ইলেকট্রন এবং নিউক্লিয়াস) প্রায়ই রিজিড বডি হিসাবে দেখা যায় ।
একটি রিজিড বডির অবস্থান তার ভর কেন্দ্রের অবস্থান এবং এর মনোভাব (মোট অন্তত ছয়টি প্যারামিটার) দ্বারা নির্ধারিত হয়।



গীম্বাল লক:
একটি গীম্বাল লক হল এমন একটি ঘটনা যা ঘটে যখন একটি তিন-অক্ষের গীম্বাল সিস্টেমের ঘূর্ণন অক্ষগুলি সারিবদ্ধ হয়ে যায়, যার ফলে এক ডিগ্রি স্বাধীনতার ক্ষতি হয় এবং স্বাভাবিক পদ্ধতিতে সিস্টেমটিকে নিয়ন্ত্রণ করা অসম্ভব হয়ে পড়ে। এর ফলে অপ্রত্যাশিত এবং অনিয়মিত আচরণ হতে পারে এবং অ্যারোস্পেস, রোবোটিক্স এবং ভার্চুয়াল রিয়েলিটির মতো অ্যাপ্লিকেশনগুলিতে সমস্যা হতে পারে। গীম্বাল লক অয়লারের কোণের সাথে সম্পর্কিত কারণ অয়লার কোণগুলি একটি ত্রিমাত্রিক বস্তু, যেমন একটি বিমান বা মহাকাশযান, স্থির অক্ষ সম্পর্কে তিনটি ঘূর্ণনের পরিপ্রেক্ষিতে অভিযোজনের একটি সাধারণ উপায়। যাইহোক, অয়লার কোণগুলি গীম্বাল লকের অধীন হয় যখন তিনটি কোণের মধ্যে দুটি সমান হয়ে যায়, যার ফলে সিস্টেমটি কিছুটা স্বাধীনতা হারায়। এটি বোঝার জন্য, তিনটি গীম্বাল নিয়ে গঠিত একটি সিস্টেমকে একে অপরের সাথে লম্বভাবে সাজানো কল্পনা করুন, প্রতিটি গীম্বাল তার অক্ষের চারপাশে ঘুরতে সক্ষম। যদি আমরা এই সিস্টেমের স্থিতিবিন্যাস বর্ণনা করার জন্য অয়লার কোণ ব্যবহার করি তবে আমাদের তিনটি কোণ নির্দিষ্ট করতে হবে: প্রথম কোণটি নির্দিষ্ট উল্লম্ব অক্ষের চারপাশে সবচেয়ে বাইরের গীম্বালের ঘূর্ণনকে প্রতিনিধিত্ব করে, দ্বিতীয় কোণটি নতুন অনুভূমিকটির চারপাশে মধ্যবর্তী গীম্বালের ঘূর্ণনকে প্রতিনিধিত্ব করে। অক্ষ, এবং তৃতীয় কোণটি নতুন অনুদৈর্ঘ্য অক্ষের চারপাশে অন্তরতম গীম্বালের ঘূর্ণনকে প্রতিনিধিত্ব করে। যাইহোক, যখন দ্বিতীয় কোণটি 90 ডিগ্রি হয়, তখন সবচেয়ে বাইরের এবং ভিতরের গিম্বলগুলি সারিবদ্ধ হয়ে যায়, যার ফলে এক ডিগ্রি স্বাধীনতা হারায়। এটিকে গীম্বাল লক বলা হয়, এবং এর মানে হল যে অয়লার অ্যাঙ্গেল ব্যবহার করে সিস্টেমটি আর স্বাভাবিক পদ্ধতিতে নিয়ন্ত্রণ করা যাবে না। গীম্বাল লক এড়ানোর জন্য, বিকল্প উপস্থাপনা যেমন কোয়াটারনিয়ন বা রোটেশন ম্যাট্রিক্স ব্যবহার করা যেতে পারে।


গীম্বাল লক সার সংক্ষেপঃ

Gimbal লক হল একটি সমস্যা যা 3D স্পেসে একটি রিজিড বডির স্থিতিবিন্যাস উপস্থাপন করার জন্য অয়লার অ্যাঙ্গেল ব্যবহার করার সময় ঘটতে পারে, যার ফলে এক ডিগ্রী স্বাধীনতার ক্ষতি হয় এবং নির্দিষ্ট অভিযোজন বর্ণনা করা অসম্ভব হয়ে পড়ে। এটি কিছু অ্যাপ্লিকেশনে অপ্রত্যাশিত আচরণ এবং ভুলতার দিকে নিয়ে যেতে পারে এবং এই সমস্যাটি এড়াতে প্রায়শই বিকল্প উপস্থাপনা, যেমন quaternions ব্যবহার করা হয়।




Quaternion:

Quaternions হল 3D স্পেসে একটি রিজিড বডির স্থিতিবিন্যাস বর্ণনা করার জন্য অয়লার কোণের একটি বিকল্প উপস্থাপনা। অয়লার অ্যাঙ্গেলের বিপরীতে, কোয়াটার্নিয়নগুলি জিম্বাল লকের সমস্যায় ভুগে না এবং নির্দিষ্ট কিছু অ্যাপ্লিকেশনের জন্য সংখ্যাগতভাবে স্থিতিশীল এবং দক্ষ।

Quaternions হল একটি গাণিতিক গঠন যা জটিল সংখ্যার ধারণাকে 4 মাত্রায় প্রসারিত করে। এগুলি ঘূর্ণনের অক্ষকে প্রতিনিধিত্ব করে এমন একটি ভেক্টর এবং ঘূর্ণনের কোণকে প্রতিনিধিত্ব করে এমন একটি স্কেলার নির্দিষ্ট করে 3D স্পেসে ঘূর্ণন উপস্থাপন করতে ব্যবহার করা যেতে পারে।

যদিও কোয়াটারনিয়ন অয়লার কোণের তুলনায় কম স্বজ্ঞাত হতে পারে, তারা কম্পিউটার গ্রাফিক্স, রোবোটিক্স এবং মহাকাশ সহ অনেক অ্যাপ্লিকেশনে ক্রমশ জনপ্রিয় হয়ে উঠেছে। তারা স্থিতিবিন্যাসগুলির মধ্যে মসৃণ ইন্টারপোলেশন, আরও দক্ষ গণনা এবং আরও ভাল সংখ্যাগত স্থিতিশীলতার মতো সুবিধাগুলি অফার করে। যাইহোক, তারা অয়লার কোণগুলির তুলনায় বোঝা এবং কাজ করা আরও চ্যালেঞ্জিং হতে পারে এবং কোয়াটারনিয়ন বীজগণিতের সাথে কিছু পরিচিতি প্রয়োজন।




কৌণিক ভরবেগ সংরক্ষণ চাকা:
কৌণিক ভরবেগ সংরক্ষণ হল পদার্থবিজ্ঞানের একটি মৌলিক নীতি যা বলে যে একটি সিস্টেমের মোট কৌণিক ভরবেগ স্থির থাকে যদি সিস্টেমে কোনো বাহ্যিক টর্ক কাজ না করে। এই নীতিটি একটি উদাহরণ হিসাবে একটি চরকা ব্যবহার করে চিত্রিত করা যেতে পারে।
একটি চাকা বিবেচনা করুন যা প্রাথমিকভাবে বিশ্রামে থাকে এবং তারপরে এটি একটি নির্দিষ্ট দিকে ঘোরানো হয়। চাকা ঘোরার সাথে সাথে এটি কৌণিক গতি লাভ করে, যা এর ঘূর্ণন গতির একটি পরিমাপ। চাকার কৌণিক ভরবেগ তার জড়তার মুহূর্ত এবং এর কৌণিক বেগের সমানুপাতিক।
যদি চাকার উপর কোন বাহ্যিক টর্ক কাজ না করে, তাহলে চাকার কৌণিক ভরবেগ স্থির থাকে। এর মানে হল যে যদি চাকাটি একটি নির্দিষ্ট দিকে ঘুরতে থাকে, তবে এটি সেই দিকে ঘুরতে থাকবে যদি না বাইরের টর্ক দ্বারা কাজ করা হয়। কৌণিক ভরবেগের সংরক্ষণ অনেক দৈনন্দিন পরিস্থিতিতে লক্ষ্য করা যায়, যেমন একটি ঘূর্ণায়মান শীর্ষ যা তার কৌণিক ভরবেগ সংরক্ষণের কারণে সোজা থাকে।
সংক্ষেপে, কৌণিক ভরবেগ সংরক্ষণ হল পদার্থবিদ্যার একটি গুরুত্বপূর্ণ নীতি যা চাকার মতো ঘূর্ণায়মান বস্তুর ক্ষেত্রে প্রযোজ্য। এটি বলে যে একটি সিস্টেমের মোট কৌণিক ভরবেগ স্থির থাকে যদি না একটি বহিরাগত টর্ক দ্বারা কাজ করা হয়.

অয়লার অ্যাঙ্গেলের ব্যবহারিক প্রয়োগ:

মহাকাশ, রোবোটিক্স, কম্পিউটার গ্রাফিক্স এবং ভার্চুয়াল রিয়েলিটি সহ বিস্তৃত ক্ষেত্রে অয়লার অ্যাঙ্গেলের ব্যবহারিক প্রয়োগ রয়েছে। এখানে কিছু উদাহরণঃ:

• মহাকাশ: মহাকাশযান, বিমান এবং ক্ষেপণাস্ত্রের অভিযোজন নিয়ন্ত্রণ করতে অয়লার কোণ ব্যবহার করা হয়। এগুলি ফ্লাইট কন্ট্রোল সিস্টেমে ব্যবহৃত হয় স্থলের সাপেক্ষে গাড়ির অভিযোজন গণনা করতে এবং বাহ্যিক শক্তির প্রতিক্রিয়ায় গাড়ির মনোভাব সামঞ্জস্য করতে।

• রোবোটিক্স: রোবোটিক্সে অয়লার অ্যাঙ্গেল ব্যবহার করা হয় রোবট অস্ত্র এবং গ্রিপারের অভিযোজন নিয়ন্ত্রণ করতে। এগুলি রোবটের শেষ প্রভাবকের অভিযোজন গণনা করতে এবং পরিবর্তিত অবস্থার প্রতিক্রিয়ায় রোবটের অবস্থান এবং অভিযোজন সামঞ্জস্য করতে ব্যবহৃত হয়।

• কম্পিউটার গ্রাফিক্স: অক্ষর এবং বস্তুর অভিযোজন নিয়ন্ত্রণ করতে 3D অ্যানিমেশন এবং ভিডিও গেমগুলিতে অয়লার অ্যাঙ্গেল ব্যবহার করা হয়। এগুলি চরিত্র বা বস্তুর পছন্দসই ভঙ্গি বা গতি অর্জনের জন্য প্রয়োজনীয় ঘূর্ণনগুলি নির্দিষ্ট করতে ব্যবহৃত হয়।

• ভার্চুয়াল বাস্তবতা: ব্যবহারকারীর মাথা বা হাতের অভিযোজন ট্র্যাক করতে ভার্চুয়াল রিয়েলিটি অ্যাপ্লিকেশনগুলিতে অয়লার অ্যাঙ্গেল ব্যবহার করা হয়। এগুলি ভার্চুয়াল ক্যামেরা বা বস্তুর অবস্থান এবং অভিযোজন গণনা করতে এবং ব্যবহারকারীর গতিবিধির প্রতিক্রিয়া হিসাবে ব্যবহারকারীর কাছে প্রদর্শিত চিত্র সামঞ্জস্য করতে ব্যবহৃত হয়।

সামগ্রিকভাবে, অয়লার কোণগুলি 3D স্পেসে একটি রিজিড বডির অভিযোজন উপস্থাপন করার জন্য একটি সুবিধাজনক এবং স্বজ্ঞাত উপায় প্রদান করে এবং অনেক ব্যবহারিক অ্যাপ্লিকেশনে ব্যাপকভাবে ব্যবহৃত হয়।




মহাকাশের ক্ষেত্রে অয়লার অ্যাঙ্গেল:


মহাকাশের ক্ষেত্রে অয়লার অ্যাঙ্গেলের বিভিন্ন গুরুত্বপূর্ণ ব্যবহার রয়েছে। এখানে কিছু উদাহরণঃ

Attitude নির্ধারণ: অয়লার কোণগুলি একটি বিমান, মহাকাশযান বা ক্ষেপণাস্ত্রের অভিযোজন বা মনোভাব নির্ধারণ করতে ব্যবহৃত হয়। অ্যাক্সিলোমিটার, জাইরোস্কোপ এবং ম্যাগনেটোমিটারের মতো সেন্সর ব্যবহার করে গাড়ির অভিযোজন গণনা করা যেতে পারে এবং অয়লার কোণের একটি সেট হিসাবে প্রকাশ করা যেতে পারে।

ফ্লাইট নিয়ন্ত্রণ: গাড়ির মনোভাব সামঞ্জস্য করতে বিমান এবং মহাকাশযানের নিয়ন্ত্রণ ব্যবস্থায় অয়লার কোণ ব্যবহার করা হয়। অয়লার কোণগুলি প্রয়োজনীয় নিয়ন্ত্রণ ইনপুটগুলি গণনা করতে ব্যবহার করা যেতে পারে, যেমন থ্রাস্টের পরিবর্তন বা নিয়ন্ত্রণ পৃষ্ঠের বিচ্যুতি।

ট্র্যাজেক্টরি অ্যানালাইসিস: অয়লার অ্যাঙ্গেলগুলি ফ্লাইটে একটি গাড়ির গতিপথ বিশ্লেষণ করতে ব্যবহৃত হয়। যে কোনো সময়ে গাড়ির অভিযোজন জানার মাধ্যমে, স্থলের সাপেক্ষে এর অবস্থান এবং বেগ নির্ণয় করা এবং এর ভবিষ্যৎ পথের পূর্বাভাস দেওয়া সম্ভব।

কৌশল পরিকল্পনা: অয়লার অ্যাঙ্গেলগুলি কৌশলগুলির পরিকল্পনা এবং কার্যকর করার জন্য ব্যবহার করা হয় যেমন টার্ন, রোল এবং পিচ পরিবর্তন। পছন্দসই অয়লার কোণগুলি নির্দিষ্ট করে, নিয়ন্ত্রণ ব্যবস্থা পছন্দসই কৌশল অর্জনের জন্য প্রয়োজনীয় নিয়ন্ত্রণ ইনপুটগুলি গণনা করতে পারে।

সামগ্রিকভাবে, অয়লার কোণগুলি ফ্লাইটে একটি গাড়ির অভিযোজন উপস্থাপন করার জন্য একটি সুবিধাজনক এবং স্বজ্ঞাত উপায় প্রদান করে এবং মহাকাশ ব্যবস্থার সঠিক নিয়ন্ত্রণ এবং বিশ্লেষণের জন্য প্রয়োজনীয়।

শর্ট সামারিঃ
1. অয়লার কোণ: একটি নির্দিষ্ট স্থানাঙ্ক সিস্টেমের সাথে 3D স্পেসে একটি রিজিড বডির অভিযোজন বর্ণনা করতে ব্যবহৃত তিনটি কোণের একটি সেট।
2. সম্পূর্ণ ঘূর্ণন: তিনটি ভিন্ন অক্ষের চারপাশে তিনটি অয়লার কোণ দ্বারা একটি রিজিড বডির একটি ঘূর্ণন।
3. ঘূর্ণনের অক্ষ: তিনটি অক্ষ যার চারপাশে ঘূর্ণন সঞ্চালিত হয়, সাধারণত x, y এবং z হিসাবে চিহ্নিত করা হয়।
4. ঘূর্ণনের ক্রম: যে ক্রমে ঘূর্ণনগুলি প্রয়োগ করা হয়, যা নির্বাচিত নির্দিষ্ট নিয়মের উপর নির্ভর করে পরিবর্তিত হতে পারে।
5. কনভেনশন: অয়লার কোণ সংজ্ঞায়িত করার বিভিন্ন উপায়, যেমন ZYX কনভেনশন, XYZ কনভেনশন এবং ZXZ কনভেনশন।
6. ঘূর্ণন ম্যাট্রিক্স: একটি 3x3 ম্যাট্রিক্স যা অয়লার কোণ ব্যবহার করে একটি সম্পূর্ণ ঘূর্ণনের পরে রিজিড বডির ফলাফলের অভিযোজন উপস্থাপন করে।
7. Gimbal লক: একটি সমস্যা যা অয়লার কোণে ঘটতে পারে যখন দ্বিতীয় ঘূর্ণন নতুন y-অক্ষকে মূল z-অক্ষের সাথে সারিবদ্ধ করে, যার ফলে এক ডিগ্রি স্বাধীনতার ক্ষতি হয়।
8. Quaternions: অয়লার অ্যাঙ্গেলের একটি বিকল্প উপস্থাপনা যা জিম্বাল লকের সমস্যা এড়ায় এবং প্রায়শই কম্পিউটার গ্রাফিক্স এবং রোবোটিক্স অ্যাপ্লিকেশনগুলিতে ব্যবহৃত হয়।

০ টি +০/-০