| নির্বাচিত পোস্ট | লগইন | রেজিস্ট্রেশন করুন | রিফ্রেস |
আমরা সবাই তো বৃত্ত দেখেছি। বৃত্ত দেখতে একদম নিখুঁত গোল। তাই না?
আচ্ছা, তবে বলুন তো বৃত্ত কাকে বলে? বৃত্তের সার্বজনীন সংজ্ঞা দেওয়াটা একটু কঠিনই। তবুও চেষ্টা করা যাক।
ধরা যাক, একটি নির্দিষ্ট তলের ওপর O একটি স্থির ও P একটি চলমান বিন্দু। এখন O কে কেন্দ্র করে যদি P বিন্দু ঐ তল বরাবর এমনভাবে আবর্তন করে যে, O বিন্দু থেকে ঐ তল বরাবর P এর ন্যূনতম দূরত্ব সর্বদা ধ্ৰুব হয়, তাহলে চলমান বিন্দুটি অনবরত আবর্তন করায় যে জ্যামিতিক চিত্র তৈরি হয়, তাকে বৃত্ত বলে। চলমান বিন্দুর আবর্তন পথটিকে বৃত্তের পরিধি বলে। O কে বলা হয় বৃত্তের কেন্দ্র এবং কেন্দ্র থেকে ঐ তল বরাবর P বিন্দুর ন্যূনতম দূরত্বকে বৃত্তের ব্যাসার্ধ বলা হয়। লক্ষ্য করুন, আমি বারবার 'তল বরাবর' শব্দটি ব্যবহার করেছি। এটি কিন্তু জ্যামিতিতে খুবই গুরুত্বপূর্ণ একটা ব্যাপার!
বৃত্তের কিছু বৈশিষ্ট্য রয়েছে। যেমন:
(ক) কোন বৃত্ত যদি একটি সমতলে থাকে, তবে এটি তার কেন্দ্রে ৩৬০° কোণ তৈরি করে।
(খ) নির্দিষ্ট তলে অবস্থিত সকল বৃত্তের পরিধি ও ব্যাসের অনুপাত একটি ধ্রুব সংখ্যা। একে π (পাই) বলা হয়। π একটি অমূলদ সংখ্যা এবং একে কখনোই কোন বীজগাণিতিক সমীকরণের মূল হিসেবে প্রকাশ করা যাবে না। সমতলে অবস্থিত সকল বৃত্তের জন্য π এর মান নিচে বেশ কয়েক ঘর পর্যন্ত দিচ্ছি। অন্যান্য তলের জন্য π এর এই মান কম বা বেশি হতে পারে।
π=3.1415926535897932384626433832795028841971693993751058.....
এখন, বৃত্তের ব্যাস যদি D হয়, এবং পরিধি S হয়, তবে আমরা পেলাম, S/D=π অর্থাত্ S=πD,
বৃত্তের ব্যাসার্ধ R হলে, ব্যাস D=2R, কাজেই S=2π
আশা করি, এবার বুঝতে পেরেছেন, কীভাবে পরিধির সূত্র আসল!
(গ) বৃত্তের ক্ষেত্রফল নির্ণয় বেশ জটিল। আর্কিমিডিস
প্রথমে সমতলে থাকা বৃত্তের ক্ষেত্রফলের জন্য সূত্ৰ বের করেছেন।
চিন্তা করুন, একটি সমতলস্থ বৃত্তের পরিধিকে সমান X ভাগে ভাগ করলাম। X খুব বড় এবং এটি বৃত্তকে অসংখ্য ক্ষুদ্র ক্ষুদ্র S/X (S=পরিধি) দৈঘ্যের চাপে বিভক্ত করেছে। চাপের প্রান্তদ্বয়কে কেন্দ্রের সাথে যোগ করলাম। তাহলে X সংখ্যক ক্ষুদ্র ক্ষুদ্র ত্রিভুজ গঠিত হলো।
প্রতিটি ত্রিভুজের ক্ষেত্রফল=০.৫*ভূমি*উচ্চতা
এখানে ভুমিকে চাপের দৈর্ঘ্যের প্রায় সমান ধরা যায়। উচ্চতাকে ব্যাসার্ধ R ধরা যায়।
তাই ক্ষেত্রফল Δ=0.5*(S/X).R=0.5*2πR.R/X= πR²/X
কাজেই বৃত্তের ক্ষেত্রফল হবে ΣΔ=Δ*X= πR²
অর্থাৎ বৃত্তের ক্ষেত্রফল= πR²
অনেক বড় একটা পোস্ট হয়ে গেলো! সবাইকে পড়ার জন্য ধন্যবাদ। 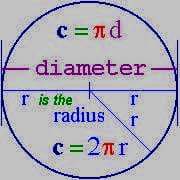
©somewhere in net ltd.
১| ২৬ শে জুলাই, ২০১৬ রাত ২:৪৪
২৬ শে জুলাই, ২০১৬ রাত ২:৪৪
মহা সমন্বয় বলেছেন: বৃত্ত অবশ্যই ভাবায়, যাবতীয় শক্তি নিহীত রয়েছে এই বৃত্তের মধ্যেই।
সামহয়্যারইন ব্লগে আপনাকে স্বাগতম।