রীমান হাইপোথিসিস উপাখ্যান

২৭ শে এপ্রিল, ২০২১ দুপুর ২:০৬

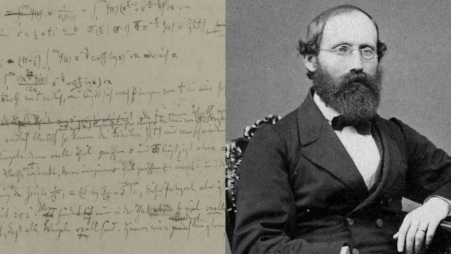
কর্নেল বিশ্ববিদ্যালয়ের জ্যোাতির্বিজ্ঞানী এবং বিজ্ঞান লেখক কার্ল সাগান কে ভারতের জ্যোতিঃপদার্থবিদ জয়ন্তবিষ্ণু নারলিকার জানতে চেয়েছিলেন ‘ই-টি' অর্থাৎ ভিনগ্রহের জীবের যদি কোনও দিন দেখা মেলেই, তাহলে ওরা পৃথিবীর মানুষের চেয়ে কম না বেশী বুদ্ধিমান তা যাচাই করার উপায় কি ? সাগানের অতি সহজ উত্তর : কেন ওদের জিজ্ঞেস করবো ফারমার শেষ প্রতিপাদ্য ওরা প্রমাণ করে ফেলেছে কিনা? নারলিকার সাগানের জবাবে সন্তুষ্ট হতে পারেন নি। তার মতে গণিতের সবচেয়ে নামী সমস্যা হিসেবে বিবেচিত হলে ও ফার্মার শেষ প্রতিপাদ্য সবচেয়ে গুরুতর প্রশ্ন।

ঠিক তাই। সাগানের পালটা প্রশ্নের জবাবে নারলিকার ‘ই-টি'-দের যেটা জিজ্ঞেস করতে ইচ্ছুক বলে জানিয়েছিলেন সেটা আর ও অনেক জরুরী সমস্যা। অন্তত। গণিতজ্ঞদের নিজেদের কাছে। হ্যাঁ, নারলিকার রীমান হাইপোথিসিসের কথা বলেছিলেন। কী সেটা? এর জবাবে দু'জন জগদ্বিখ্যাত গণিতবিদের কাহিনী বলতে হয়।

জার্মান গণিতজ্ঞ ডেভিড হিলবার্ট একবার বলেছিলেন, এক হাজার বছর টানা ঘুমিয়ে থাকার পর হঠাৎ জেগে উঠলে প্রথম যে প্রশ্নটা ওঁর মাথায় আসবে তা হল, রীমান হাইপোথিসিস কি প্রমাণিত হয়েছে? আর জি, এইচ, হার্ডি -সেই ব্রিটিশ গণিতজ্ঞ, হতভাগ্য ভারতীয় শ্রীনিবাস রামানুজমের প্রতি তা যিনি প্রথম উপলব্ধি করেছিলেন তার সম্পর্কে রীমান হাইপোথিসিস নিয়ে চাল মজাদার কাহিনী। হার্ডির নাস্তিকতা সুবিদিত ছিল তার বন্ধুমহলে । প্রার্থনা সভা নয়ই, এমনকি আচার-অনুষ্ঠানেও চ্যাপেলের ছায়া মাড়াতেন না তিনিও রীমান হাইপোথিসিস নিয়ে ঈশ্বরের সঙ্গে মশকরা করতে ছাড়েন নি। স্ক্যান্ডিনেভিয়া থেকে নর্থ সী হয়ে ইংল্যান্ডে আসার সময় একবার প্রবল ঝড়ের মধ্যে যায় ওঁর লঞ্চ। মৃত্যুনিশ্চিত জেনে উনি চিঠি লেখেন ওর এক বন্ধুর কাছে। মাত্র এক লাইনের। “রীমান হাইপোথিসিস প্রমাণ করে ফেলেছি। ইতি, হার্ডি। “ ওঁর যুক্তি পরিষ্কার । ঈশ্বর ওঁকে কিছুতেই অঙ্কের “মোস্ট ইমপরট্যান্ট আনসলভড প্রবলেম “ সমাধানের কৃতিত্ব নিয়ে মরতে দেবেন না। তার চেয়ে বরং সাক্ষাৎ মৃত্যুর হাত থেকে বাঁচিয়ে (লঞ্চডুবি হলে পোস্টকার্ড বন্ধুর কাছে পৌছত কি করে কে জানে!) দেবেন ।

রীমান হাইপোথিসিসের মাহাত্ম্য বুঝাতে প্রথমে তাকানো দরকার মৌলিক সংখ্যার দিকে। মৌলিক সংখ্যা কোনগুলি ? 2 , 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37... কি বৈশিষ্ট্য ওদের? ওরা কেউই অন্য সংখ্যা দ্বারা পুরোপুরি বিভাজ্য নয়। সংখ্যারাজ্যে ওরা যেন এক এবং অদ্বিতীয়। তাই মৌলিক। অন্য যে কোনও সংখ্যাই (যাদের বলা হয় যৌগিক) একাধিক মৌলিক সংখ্যার গুণফল।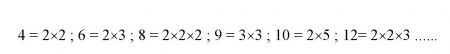

রসায়নবিদের কাছে যেমন হাইড্রোজেন, অক্সিজেন, কার্বন বা ইত্যদি মৌল যা দিয়ে সমস্ত পদার্থ তৈরি আর পদার্থবিজ্ঞানীর কাছে যেমন কোয়ার্ক কিংবা লেপটন- যা সমস্ত মৌলকণার উপাদান- সংখ্যাবিদের কাছে তেমনি মৌলিক সংখ্যা। এর আকর্ষণ অপরিসীম। কারণ, এ সব কিছুর আদি, মূল। এই মৌলিক সংখ্যা বিষয়ে একাধিক অনুমান বা প্রতিপাদ্য রীতিমত আকর্ষণীয়। এদের কোনটির স্বপক্ষে প্রমাণ ইতিমধ্যেই পাওয়া গিয়েছে, আবার কোনওটি এ প্রমাণ-বিনে দাপিয়ে বেড়াচ্ছে। যেমন ধরুন মৌলিক সংখ্যা বিষয়ে ফার্মা-র বিশেষ প্রতিপাদ্যটি। মৌলিক সংখ্যাগুলোকে ফার্মা ভাগ করেছিলেন দুটো শ্রেণীতে-

5, 13, 17, 29, 37, 41........ অর্থাৎ, যেগুলোকে ৪ দিয়ে ভাগ করলে ভাগশেষ থাকে ১,
আর- 3, 7, 11, 19, 23, 31......
যেগুলোর বেলায় ওই ভাগশেষ হবে 3 ; এখন মৌলিক সংখ্যার এই দুটো শ্রেণীর মধ্যে ফার্মা বিশেষ একটা পার্থক্য লক্ষ করেছিলেন। আর সেটা হল এই যে, প্রথম শ্রেণীর প্রতিটি সংখ্যাই এক জোড়া সংখ্যার বর্গের সমষ্টি। যেমন-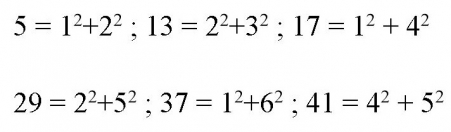

কিন্তু দ্বিতীয় শ্রেণীর মৌলিক সংখ্যাগুলোকে কখনও ওভাবে লেখা যায় না। কেন, সেটা প্রমাণিত হয়েছে। যদিও সেই দীর্ঘ প্রমাণের পুরোটা এখানে ফার্মা-র শেষ প্রতিপাদ্যের ব্যাপারে অ্যান্ড্রু ওয়াইলস- এর ব্যাখার মতই সবিস্তারে জানানো সম্ভব নয়। মৌলিক সংখ্যা সংক্রান্ত আরেকটা প্রতিপাদ্য- যা কিনা শুনতে জলবৎ তরলং- তার এখনও প্রমাণ দিয়ে উঠতে পারেন নি কেউ। ১৭৪২ খ্রিস্টাব্দে লিওনার্ড অয়লারকে লেখা এক চিঠিতে গণিতজ্ঞ ক্রিশ্চিয়ান গোল্ডবাক প্রথম ওটার উল্লেখ করেছিলেন। উনি দেখিয়েছিলেন, প্রতিটি জোড় সংখ্যাই দুটো মৌলিক সংখ্যার সমষ্টি।
যেমন-

4 = 2+2
8 = 3+5
12 = 5+7 .....

কেন এমন হয়?

এই অদ্ভুত ব্যাপারটা- যা ‘গোল্ডবাক কনজেকচার’ নামে খ্যাত- তা মোটেই খটমট নয় বুঝতে। প্রায় ফার্মা’র শেষ প্রতিপাদ্যের মত কিংবদন্তীতে পরিণত হয় নি। কেন হয় নি তার উত্তর বোধ হয় এইটেই যে, গোল্ডবাক অয়লারকে চিঠিতে লেখেন নি, ‘আমি প্রমাণটা জানি। এই চিঠিতে ধরবে না বলে লিখলুম না।’’
মৌলিক সংখ্যার বিষয়ে যে প্রতিপাদ্যটি পন্ডিত ইউক্লিড কয়েক হাজার বছর আগে প্রমাণ করেছিলেন সেটার দিকে তাকিয়ে আমরা এখনও বিস্মিত হই। অবাক হই প্রমাণ কৌশলের সারল্যে। প্রথমে প্রশ্নটায় আসি। মৌলিক সংখ্যার রাজ্যের দিকে তাকিয়ে দেখুন একবার :
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41
43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101.....

প্রথমে যে চারটি মৌলিক সংখ্যা তারা বেশ কাছাকাছি। পরের চারটে কিন্তু ততটা কাছাকাছি নয়। সংখ্যাগুলো বড় হয়ে গেলে মৌলিক সদস্যেরা একে অন্যের চেয়ে বেশ দূরে চলে যায়। তখন পর পর দুটো মৌলিক সংখ্যার ব্যবধান রীতিমত বেড়ে যায়।

যেমন 10,000,000 আর 10,000,100 এই দুটো সংখ্যার মধ্যে মাত্র দুটো মৌলিক সংখ্যা পাওয়া যাবে। এখন প্রশ্ন, তাহলে ক্রমশ বড়, আরও বড় সংখ্যার দিকে এগোলে মৌলিক সদস্যের ভাঁড়ার কি এক সময় শূন্য হয়ে যাবে? প্রশ্নটার জবাব দিয়েছিলেন ইউক্লিড। বুঝিয়ে দিয়েছিলেন, না, শেষ বা সবচেয়ে বড় মৌলিক সংখ্যা বলে কিছু নেই। স্বাভাবিক সংখ্যার সাপ্লাই যেমন ফুরোয় না, তেমনি মৌলিক সংখ্যা একটা সময়ে শেষ হয়ে যায় না। একটা বড়সড় মৌলিক সংখ্যার পরেও আরেকটা মৌলিক সংখ্যা আছে। তা সেটা প্রথমটির চেয়ে যত বেশী দূরবর্তীই হোক না কেন।

ব্যাপারটা প্রমাণে ইউক্লিড প্রথমে ধরে নেন উল্টোটা। অর্থাৎ, শেষতম বা সবচেয়ে বড় কোনও মৌলিক সংখ্যা আছে। এবারে দেখা যাক কী হয়। ধরা যাক, কল্পিত সর্বোচ্চ মৌলিক সংখ্যাটি N এবারে প্রথম থেকে শুরু করে এবং এই N কে নিয়ে যতগুলো মৌলিক সংখ্যা পাওয়া যাচ্ছে সেগুলো গুণ করে ফেলা যাক। তাহলে পাওয়া গেল....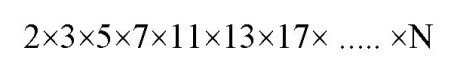
এবারে এর সঙ্গে 1 যোগ করলে যে সংখ্যাটি পাওয়া যাচ্ছে সেটি হল ......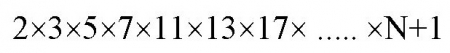


এই যে নতুন সংখ্যাটি পাওয়া গেল সেটাকে কিন্তু 2,3,5,7,11,13,17, ........ N এর কোনওটি দ্বারা ভাগ করলে মিলবে না। সব ক্ষেত্রেই ভাগ শেষ থাকবে। আর সেটা হবে 1 ; তাহলে এই নতুন সংখ্যাটি দাঁড়াচ্ছে এমন যে তাকে N পর্যন্ত কোনও মৌলিক সংখ্যা দিয়ে ভাগ করলে মিলে যায় না। সুতরাং, প্রথমে যে ধারণা নিয়ে শুরু করা গিয়েছিল N সবোচ্চ মৌলিক সংখ্যা ......... সেটা ঠিক নয়। অর্থাৎ, শেষ মৌলিক সংখ্যা বলে কিছু নেই। বড়-র ওপরেও আরও বড় মৌলিক সংখ্যা আছে ।

শেষতম মৌলিক সংখ্যা থাকলেই বোধ হয় ভাল হত। তাহলে অন্তত অনেক দিন আগে বন্ধ হয়ে যেত ও বিষয়ে বুদ্ধির ব্যায়ামটা। যুগে যুগে গণিতজ্ঞরা কি কম লড়েছেন বিষয়টা নিয়ে ! পর পর মৌলিক সংখ্যা বানানোর একটা সাধারণ ফমুর্লা আবিস্কার করা যায় কিনা তা নিয়ে গণিতজ্ঞরা ভেবেছেন নানা যুগে। আর, বলাই বাহুল্য, সব ভাবনা জলে গেছে মৌলিক সংখ্যার খামখেয়ালি চরিত্রে।

উদাহরণ দিচ্ছি একটা । এই ফর্মুলাটার দিকে তাকিয়ে দেখুন ।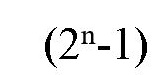

n- এর মান 2, 3, 5, 7 (অর্থাৎ মৌলিক শ্রেণী) হলে একেকটা মৌলিক সংখ্যা পাওয়া যাবে। যেমন-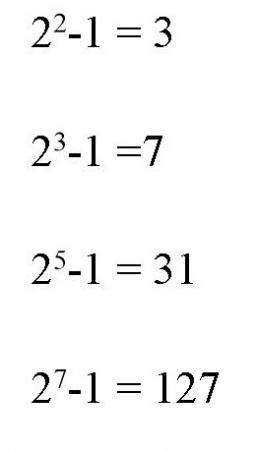




কিন্তু n = 11 বসিয়ে দেখুন কি হয়।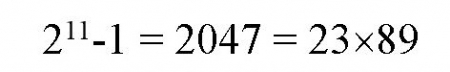


অর্থাৎ এটা আর মৌলিক সংখ্যা নয়।

মৌলিক সংখ্যা নিয়ে মাথা ঘামাতে বসে ফার্মাও প্রথমে মনে করেছিলেন, বুঝিবা, উনি পেয়ে গেছেন ফর্মুলাটা । ওঁর মতে যেটা কিনা ,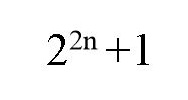

এবারে n = 0,1,2,3,4 ........................ বসিয়ে দেখা যাক।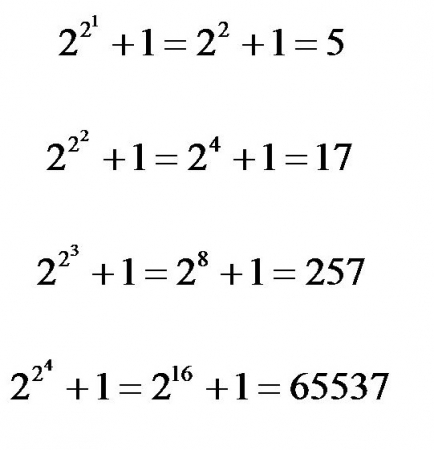



হ্যাঁ, এরা মৌলিক : কিন্তু, দুর্ভাগ্য ফার্মা-র, এর পরেরটা আর মৌলিক সংখ্যা নয় , অর্থাৎ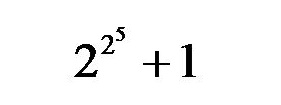

এটা আর মৌলিক সংখ্যা নয়

কারণ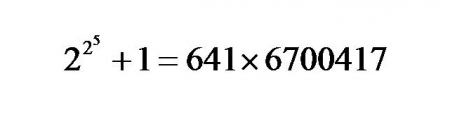




মৌলিক সংখ্যাগুলোর নিজেদের মধ্যে কোনও সম্পর্ক যতই দুলর্ভ হয়ে পড়ে, ততই গণিতজ্ঞদের জেদ বাড়ে একটা কোনও ধারা আবিষ্কারের। বাড়বেই। আপাত অমিল জিনিসের মধ্যে মিল খুঁজে পাওয়ার নামই যে বিজ্ঞান। গাছ থেকে আপেল পড়া আর আকাশে শুক্র গ্রহের জায়গা বদল দুটো আলাদা ব্যাপার। অন্তত প্রথম দৃষ্টিতে। আলাদা যে নয়, সেটা বলে দিয়েছে বিজ্ঞান। আর বলে দিয়েছে বলেই, বিজ্ঞান এত আকর্ষণীয়। ভারতীয় গণিতপ্রতিভা শ্রীনিবাস রামানুজমও এক সময়ে মৌলিক সংখ্যা বিষয়ে ব্যর্থ প্রয়াসে মগ্ন ছিলেন কোনও একটা সংখ্যা হলে তার আগে ঠিক কতগুলো মৌলিক সংখ্যা পাওয়া যাবে সে বিষয়ে। রামানুজম ভেবেছিলেন, এ ব্যাপারে একটা ফমুর্লা বুঝিবা উনি পেয়ে গেছেন। হার্ডিকে যে একগুচ্ছ ফর্মুলা উনি চিঠি লিখে পাঠিয়েছিলেন- যে চিঠি পড়ে ওঁর প্রতিভার পরিচয় পান ওই ব্রিটিশ গণিতজ্ঞ- তার মধ্যেই রামানুজম ওই ব্যাপারটা উল্লেখ করেছিলেন। ওঁর উদ্ভাবিত ফর্মুলা যে ঠিক নয় সেটা হার্ডি বুঝতে পেরেছিলেন।

বলতে কি, একটা সংখ্যা আগে পর্যন্ত ঠিক কটা মৌলিক সংখ্যা রয়েছে তা বাতলানো কোনও ফর্মুলা এখনও পর্যন্ত কেউই বের করতে পারেন নি। তবে, ১৮৫৯ সালে জার্মান গণিতজ্ঞ বার্নার্ড রীমন একটা ফর্মুলা বের করেন তার সাহায্যে মৌলিক সংখ্যাগুলোর রাজ্যে একটা বিন্যাস বা ধারা লক্ষ করা যায়। একটা বিরাট বড় অঙ্কের সংখ্যার আগে পর্যন্ত কতগুলো মৌলিক সংখ্যা আছে সেটা রীমানরে ফর্মুলায় মোটামুটি ( ঠিক ঠিক নয় কিন্তু ) ধরা পড়ে। এই র্ফমুলাটা হল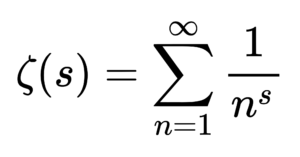




সংখ্যাগুল আসলে যা , আর ওই ফর্মুলা অনুযায়ী যা পাওয়া যাচ্ছে তার একটা তালিকা দেওয়া হল।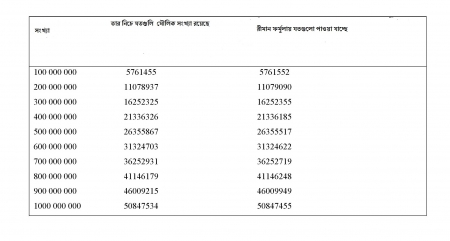


এখন এই আপাত-সফল ফর্মুলাটা কিন্তু তৈরী হয়েছে একটা অনুমান কে ধরে নিয়ে। এই সমীকরণের যুক্তিনির্ভর প্রমান আজ পর্যন্ত পৃথিবীতে কেউ করতে পারে নি । অনুমাননির্ভর একটা ফর্মুলা একটা খামখেয়ালী রাজ্যের কাজে লাগছে। কেন লাগছে তা কেউ জানেন না। যেমন জানেনা না ওই অনুমানটা সত্যি কিনা। আজ পর্যন্ত কেউ ওটার সত্যতা প্রমাণ করতে পারেন নি।

ওই অনুমানটির নামই রীমান হাইপোথিসিস ।

References : 1. Click This Link
2. Click This Link

৫ টি +১/-০