বৃত্তের উৎকেন্দ্রিকতা

১৯ শে জুলাই, ২০১৬ ভোর ৪:০৬

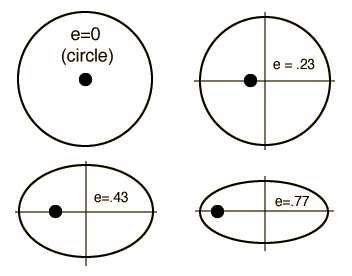
বৃত্তের উৎকেন্দ্রিকতা কত? উত্তরটা হল ০, কিন্তু কেন? যারা একটু পড়ুয়া, তারা উত্তর দেবে বৃত্তে a=b, e=√(1-b²/a²)=0.
বাহ, কতো ব্রিলিয়ান্ট আপনি!!!!! কিন্তু ব্যাপারটা কি আসলে এরকম??? উপবৃত্তের আদর্শ সমীকরণ প্রতিষ্ঠার সময়ের কথা মাথায় থাকলে এরকম উত্তর দিতেন না আপনি। ব্যাপারটা বুঝানো যাক এবার।
যেকোন দ্বিঘাত সমীকরণ (দুই চলকের) একটি কনিক অথবা যুগল সরলরেখা প্রকাশ করে। এবার mx+ny+c=0 যদি দিকাক্ষ আর (a,b) যদি ফোকাস হয়, তবে কনিকটির ওপরের যেকোন বিন্দু থেকে ফোকাস ও নিয়ামকের লম্বদূরত্ব একটি ধ্রুব সংখ্যা। আর এটিই হল উৎকেন্দ্রিকতা e. এখান থেকে সহজেই দেখানো যায়, কনিকটি
(x-a)²+(y-b)²=e².(mx+ny+c)²/(m²+n²).............(1)
এখন চিন্তা করে দেখুন, সমীকরনটির ডানপক্ষে e অশুন্য হলে - (i) যদি m,n অশুন্য হয় তবে সমীকরণে xy যুক্ত পদ চলে আসবে। (ii) যদি m ,n এর যেকোন একটি শূন্য হয় তবে সমীকরণে x²,y² এর সহগ আলাদা হবে। আর m,n দুটোই শুন্য হতে পারেনা (সরলরেখা বলে) কাজেই সমীকরণটি বৃত্ত হতে গেলে আর একটি পথই থাকে- সেটা হল e=0,অর্থাৎ উৎকেন্দ্রিকতা শূন্য। আর তখন সমীকরণ (1) দাঁড়ায় (x-a)²+(y-b)²=0 যা কিনা বিন্দু বৃত্ত!!! আপনার চিন্তায় বৃত্তটি নিশ্চয়ই বিন্দু ছিল না!!!

০ টি +০/-০